くろべえ: 1999

1999年12月16日木曜日

徹夜あけ

結局昨日は徹夜で採点した．期末テストは返せたけど，10月の小テストはあとまわしになった．採点そのものは4時ころ終了したが，パソコンに入力，成績処理に6時までかかった．

1999年12月9日木曜日

1999年2学期数学Ⅲ一斉テスト

2学期末テスト．

今回の試験範囲は

怒涛の１３８ページ！！

教科書ではこの138ページ分だが，教科書以上の内容を解説した50枚以上の両面印刷プリントもテスト範囲だった．生徒諸君，ご苦労様．（自分が生徒じゃなくてよかったと，本気で思うゾ）

ということで，あまりに広い試験範囲だから，計算問題は「教科書丸写し状態」で何の工夫もないまことにお恥ずかしい状態．そのかわり記述式はいろいろと論じてもらった．

pdf と TeXソース

1.等式 x +a − 3b = −2(x − 2a − 3b) を満たすベクトルx を，a, b を用いて表せ．

2.一直線上にない3 点O, A, B について，OP = sOA + tOB, s ≥ 0, t ≥ 0,
s + 2t = 3 を満たす点P の存在範囲を求めよ．

3.a = (1, 2), b = (3, 1) とする．
(1)2b −a を求めよ．
(2)2b −a の大きさを求めよ．
(3)p = (5, 1) をa, b を用いて表せ．
(4)a ·b を求めよ．
(5)a, b のなす角を求めよ．
(6)a に垂直な単位ベクトルを求めよ．

4.方向ベクトル(1, 2, −1) で点(3, 4, 2) を通る直線の方程式をパラメータ表示で表せ．

5.点(2, 3) を通り，法線ベクトルが(5, 2) である直線の方程式を求めよ．

6.中心の位置ベクトル⃗c で半径r の円|p −c| = r 上の点p0 における接線
のベクトル方程式を書け．

7.f(x) =√x において，区間0 ≤ x ≤ 1 で，平均値の定理を満たすx = c を求めよ．

8.関数y = ex − x の増加減少を調べよ．

9.関数f(x) = |x^2 − 1| の極値を求めよ．

10.曲線y = x + sin x (0 < x < 2π) の凸凹と変曲点を調べよ． 11.半径r の半球型の容器に毎秒a ずつ水を注ぐとき，深さがr/2 のときの水面の上昇速度を求めよ． 12.log 1.01 の近似値を計算せよ． 13.1/cos^2 x の原始関数を求めよ． 14.1/tan x の原始関数を求めよ． 15.x log x の原始関数を求めよ． 16.x/((x + 1)(x + 2)) の原始関数を求めよ． 17.∫[1,e](1/x)dx を求めよ． 18.∫[0,1](1/(1 + x^2)) dx を求めよ． 19.∫[1,e]log x dx を求めよ． 20.数列 1/(n + 1) + 1/(n + 2) + · · · + 1/(n + n) の極限を求めよ． 21.関数 ∫[x,x^2] f(t) dt をx について微分せよ． 22.曲線y^2 = x とy 軸，直線y = 1, y = −1 で囲まれる部分の面積を求めよ． 23.0 ≤ x ≤ π/2 の範囲で，曲線y = cos x とx 軸に挟まれる部分を，y 軸の周りに回転させてできる回転体の体積を求めよ． 24.x = 2t − 1, y = e^t + e^(−t) で表された曲線の0 ≤ t ≤ 1 の長さを求めよ． 25.微分の平均値の定理を正確にかけ．そして図形的イメージを説明せよ． 26.極値を定義せよ． 27.2 回微分可能なf(x) において，f''(a) > 0 ならばx = a で「　　　」に凸である理由を説明せよ．

28.積分∫[a,b]f(x) dx の存在を保証する定理を述べ，積分を定義せよ．

29.積分の平均値の定理を正確にかけ．そして図形的イメージを説明せよ．

30.微分積分学の基本定理を書け．

31.微分積分学の基本定理の意味を説明し，その恩恵を述べよ．

32.単なる微分の逆操作の結果である「原始関数」に「不定積分」という「積分」の名を与えた事情を考察せよ．

33.曲線(x, y) = (g(t), h(t)), α ≤ t ≤ β の長さを積分で表し，その表し方がわれわれの感覚と矛盾しない事情を，積分の存在の定理，あるいは微分積分学の基本定理の観点で説明せよ．

34.球の体積を半径で微分すると表面積になる理由を説明せよ．

linked: 1

1999年12月7日火曜日

「自分探し」へのコメント

あるBBSへ書き込みました．

自分探しの思索は大切です．
しかしそれにとらわれると不幸です．

思索を支えるのが行動です．それも困った人のための行動．
アフリカの飢餓や戦争のように，明日の命すら危うくて，自分探しの思索が出来ない人々にとっては，それができるこの国がなんと平和なことだと思いませんか？

行動といっても，身近なところから．最も苦しんでいる人を最も大切にするような世の中になるような手助けを少しずつでしながら，自分探しの思索をしてみてください．

人は心のつながりを糧に生きる生物です．結局「自分探し」といっても，人はそのつながりの中の自分しかありえません．そして心のつながりをつくるには，行動に出るしかありません．さらにその行動は「最も苦しんでいる人を支える」です．その行動の中にあなた自身が見つかるはずです．みつかったら教えてね．

苦しいときほど外に目を向ける．まるで苦しんでいる人に鞭打つようで気が引けるのですが，精神的苦悩というものは「行動」の中に解決を見出すしかないですから．

私にとって「自分」とは上記の精神を行動で表現する人間であることを20代前半で見つけました．

「自己を意識する」のは人間だけです．つまり人間の持つ理性です．これは言語を持たないほかの生物ではありえません．理性というものは感情とは別の脳の働きですから，時として心のつながりを阻害します．つまり理性で自分探しをして「言葉で表現された自分」を探そうとすると，心のつながりの喪失になりやすく，精神的な苦悩に陥りますよ．私が「行動」を強調するのはそこにあります．

ようするに私は伸びきったゴムのように「脳天気者」で，精神的苦悩を持つ人にとっては軽蔑される人間です．しかし逆に私は人助けもしないで勝手に悩んでいる人間を哀れだと思いますが．

1999年11月20日土曜日

カルトの宣伝に使われる馬鹿なマスコミ

マスコミの馬鹿さ加減というものをまた今回も感じた．
あの記者会見報道である．

オウムのじょうゆうの記者会見を思い出した．

カルトの発言をそのまま報道するのはまったくばかげている．
記者もカルトからまともな答えを引き出そうとするが，
当然キチガイなのでそんなものは出てこない．
まっとうな答えが出なければ，そんなものは公共のメディアに乗せる価値のないものである．

きっとカルト信者予備軍が「放送されるほどのカルトだ」と殺到して，
あのカルトはまた人数を増やすだろう．
オウムがじょうゆうの記者会見で人数を増やしたように．
またまた大もうけだ．

馬鹿なマスコミどもはオウム事件を全く教訓にしていない．
NHKが記者会見の報道をしないのはさすがだと思った．

カルトとは

カルトは科学や常識を否定するところから始まる．
「科学的」を装っていても結局は「呪術，オカルト」の世界だ．

現代は科学や常識が高度な社会システムとして存在しているため，
時として人間が疎外感を受けることがある．
こんなとき，その社会システムを否定するカルトがその疎外感にうまくつけこんで勢力を拡大するわけだ．
オカルトや呪術も同様で，結局はシステムからの逃避にしか過ぎないと思う．
最大にシステムを否定した結果がオウムのハルマゲドンである．
ライフなんたらも現代の医学システムを否定するところから始まっているわけで，スタートは昨今の「健康ブーム」でだろうなきっと．

私などは普段から「常識」に疑問を持ち必ず「この常識を否定するとどうか」ということを考えてる．
しかし「良識」は失わない．
常識やシステムを否定して連帯感を高めているうちに自ら良識を失った集団．それがカルトだ．

で，そのような逃避者を生む社会システムをどのように人間の手に取り戻すか．
システムは「思想」ではないので，結局人間の「本能」の赴くままに構築されゆく傾向がある．
そこに本当の思想，哲学，宗教の存在意義があるわけだ．

1999年11月17日水曜日

教師の不祥事

教師がまた破廉恥事件でつかまった．
ひとりはなんと
「ばれなきゃいいと思った．」
とほざいた．とんでもないやつだ．

子供が親の目を盗んで悪いことをしているのとまるで同じで，
ふつう大人ならば「誰も見ていなくても悪いことは悪い」と判断がつくだろうに，
と思う．
こういう大人の見てくれをしたガキを排除しないかぎり，
どんなに教育論を論じても，
机上の空論で，
教育改革は空洞化する．

不祥事は「教師以前」の人間として振る舞いだから，
教師であろうとなかろうと
「悪いことは悪い」
のだ．
防ぐためのひとつの策としては，
教師が不祥事を起こしたら二度と社会復帰できないほどの制裁を加える．
マスコミは教師や警察官の不祥事は徹底的に糾弾すべきである．

また「ばれなきゃなにやってもいい」という人間が教師をすると，
往々にしてまじめで「規則を守らせる指導」がうまく，
子供が親の前ではいい子であるように，
こういう人間は上司からも「熱心な先生」と思われるのも上手である．
さらに，規則で縛る教育ほどコストのかからぬものはない．
心で納得させるのではなく，「規則だから」と規則に教育させるのである．
その結果が，子供も「ばれなきゃなにやってもいい」，
「人に迷惑かけなきゃなにやってもいい」につながる．

教育とはいい子になる見栄のはりかたを教えるのではなく，
行動の美学を確立する手助けをするものであるはず．

1999年11月9日火曜日

麦芽乾燥

天日干しにしたいが，天気が悪いから室内で一気に乾燥．
「明日は晴れ」という天気予報もあったが，麦芽の成長は待ってくれない．
今日ストップしないとビール用短麦芽にならない．
猫を外に追い出し，部屋を掃除し，床を洗剤で洗浄し，扇風機とファンヒーターで乾燥．

3時間くらいで生乾き，乾いたところから少しずつフライパンで煎って，根を干からびさせる．このとき，強く煎れば色の黒いビールになる．

干からびた根を篩にかけて完成．

これを少しずつ使うわけだ．2kgの麦芽で大瓶15本くらいかな．

全部終わるのに6時間以上かかり，筋肉痛．次の作業はミキサーで粉砕して糖化．まぁこれは酵母の準備ができてからゆっくりやろうっと．

酵母はパン用のイーストでもいいし，私は以前キットについていたドライイースト（粉末状の仮死状態の酵母）を残していたからそれを使ってもいいのだが，せっかくだからリキッドイースト（液体の中で生きている酵母）を入手してみようかな．味がぜんぜん違うそうだ．それが手に入るまで一時中断．

キットを使うとすんげー簡単．＞自家製ビールFAQリスト

1999年11月8日月曜日

ビール造り

種まきの現場．

麦芽ちゃんたち．右側はだいぶ芽が大きくなってきた．
いわゆる「モルト」（もやし）だ．
もう今日あたり乾燥させなければなりません．
乾燥粉砕＞糖化＞発酵…とまだまだ先は長い．

いずれアップしやす．

酒税法は過去数千年にわたった人類の「酒作りの文化」を消滅させたといってよい．
酒税は「戦費調達」のため日露戦争当時に導入されたもので，税収に多くするために「個人の酒造」を禁じたものである．つまり「酒は店で買え．」
これがどれほど不合理なものかは，「おにぎりは店で買え．自宅で作るのは密造だ．」といわれたら，どうかということを考えてみればよい．これと同じことを言っているのだということである．
つまり「おにぎりを自宅で作られては，消費税収に穴があくから，必ずコンピニで購入し密造させない，違反者には懲役，罰金で処罰する．」
これを，おにぎり→酒，消費税→酒税　と読み替えたのが，酒税法である．もしこのような「おにぎり法」が施行されたら日本の弁当文化が消滅するように，酒造文化が消滅したのである．個人酒造を復活させよう．

昨日はフェンシング

の試合だった．「新人戦」というやつ．

うちは全員が1年生のチームながら，個人戦ベスト8に2名進出し，団体戦も最下位にはならなかった．来年以降が有望だ

1999年11月1日月曜日

信仰

信仰というと，現代人は「おれは信仰なんてしないよ」なんていいながら，
信仰している人間が多い．
べつに初詣に行ったり，寺で葬式出したりすることを言っているわけではない．
そんなものは信仰ではなく，しきたり，習慣である．
本気で信じているやつなどあんまりいない．
それが証拠に，「あなたは信じていますか」と聞いて
きっぱり「そうです」と胸を張る人間がどれだけいるか．

私の言うのは，科学信仰，機械信仰だ．
便利さにだまされて，疑うということをしない．
人がいいといえばそうかもしれない．
「機械は壊れない」と思っている人間が多すぎる．
これは「思っている」などという生易しいものではなく，
まったく「信仰そのもの」である．

パソコンがあれだけfreeze していても，
「こわれないもの」と思い込んでるのだからまさしく
「だまされてもだまされても正しいと思い込む信仰」としかいいようがない．
全く敬虔な機械信者としかいいようがない．

私はどうも周りから「パソコンできる」と思われているせいか，
「○○したらパソコンが止まった．どうすればいいか」という質問をよくされる．
「機械なんだからこわれるんですよ，たまには．」というと
不満のようである．

わたしなどは最大で1日に5回 freeze して reset ボタンを押したり，
reset ボタンすら効かなくて，バッテリを含む全ての電源システムを
はずしてはじめて reset することも月に数回はある．
それは本当はメーカーにクレームでもつけるべきなのだろうが，
今のところそれでデータがぶっとんだりしないからそんな面倒なことはしない．
メーカーに問い合わせたって，時間ばかりかかって要領を得ないし，
reset で．解決するのだからＯＫ．
さらに自分のミスでデータを消すことなど日常である．
だから，機械の止まるのなんて，別に平気である．

踏み切りの開いている遮断機は絶対うそだと思うから，
一時停止はしなくても電車の来ないことは必ず確認する．
「青信号」などは信じない．

盲目的な信仰が時として不幸を招くのは歴史の事実だが，
機械文明，科学技術に対する盲目的信仰は，
過去に例のないものである．

テレビをぶったたけば映るように，旅客機だってきっとそうだ．
原子力だってぶったたけば…　だから原子力はやめてほしいのだ．

1999年10月22日金曜日

防衛政務次官辞任

「議論をすることはよくないのか？」
といった，やめ方をしていた．
もしかしたら，この発言を聞いて，
「議論自体を封じ込めるのはよくない」
と思う人もいるかもしれないが，違うな．

大量殺戮の方法を議論するって言ってるんだぞこいつらは．
なーんだ，オウムと同じ穴のむじなだな．ということがよくわかる．
「殺す方法」を議論するなどとんでもない．
サリンを作る議論と，核兵器を持つ議論というのは，
全く同じであることを認識しなければならない．

殺人が好みの人物を，閣僚からはずすのは当然として，
なぜ，議員辞職に追い込めないのか．
このような人物が議員であるというのは，
松本ちずおを議員にするのと同じということだ．

核兵器は防衛ではなく侵略兵器である．
抑止力といったものは幻想でしかない．
それは核がこわいという考えから出てくる．
簡単に言うと「暴力が怖い」わけだ．
暴力は痛いけど怖くはない．
暴力には良識に基づいた言論で対抗するものだ．
核兵器の廃絶は核兵器に頼ろうとする（西村のような）
人間の心に巣食う暴力への恐怖を廃絶するしかないのだ．

あと，言論の自由というのは「言論によって刑事罰を受けない」だけであって，
殺人の言論を吐く人間を公人から排除することは，
言論の自由となんら矛盾するものではない．
今回の事件は言論の封じ込めでもなんでもなく，
閣僚辞任くらいでは不十分だ．

1999年10月21日木曜日

1999年数Bベクトル抜き打ちテスト

10月に3年生に実施した抜き打ちテスト。1学期に抜き打ちをやっているので，生徒諸君にとっては「まだかなまだかな．そろそろだぞ」という期待と不安の中実施されたテスト．

pdf と TeXソース

１．「写像」と「対応」の違いについて説明せよ．

２．命題「ある区間(a − p, a + p) をとれば区間内のすべてのx について
f(x) ≤ f(a)」の否定命題を述べよ．

３．有界と無限小を定義せよ．

４．lim x = α を「無限小」という言葉を用いて定義せよ．

５．無限小と無限小の和が無限小であることを用いて，lim(x+y) = lim x+lim y
を示せ．

６．数列　$(1+\frac{1}{n})^n$ の極限や，$2^{\sqrt{3}}$
の存在を保証する数列の定理はどのようなものか述べよ．

７．「1/n は正の数，正の数は0 ではないのに極限が0 であるのは納得できな
い．」という人に対してどのように説得しますか．

８．「はさみうちの原理」を書いてください．

９．$\lim_{x\to 0}\frac{\sin x}{x}=1$ の図形的意味を説明せよ．

10．関数の連続を定義せよ．またその定義のセンスはどんなものか．

11．最大値の定理を正確にのべよ．

12．中間値の定理を正確に述べよ．

あたった

モニター募集に応募したら，あたった．
今日は給料日だし，ただのビールは手に入ったし，気分がハイになって抜き打ちテストをやった．

1999年10月19日火曜日

生徒のＨＰより

＞　子供「へぇ、二十世紀ってこんなんだったんだ。ところで２０００年って父ちゃん何歳の時？」
＞　父親「２０歳」
＞　子供「父ちゃん、その記念すべき千年紀に何してたの？」
＞　父親「浪人してた」
＞　嫌ですねえ。これは。

時計を買った

腕時計だ．こういうものには大変なこだわりがある．
まずはロレックスであること．なんていうことでなく，
「安いこと」と「時計としての機能が整っていること」だ．

そもそも，いままで使っていたのは4年前にホームセンターで980円で
買ったものだ．
そのとき，580円のディジタル時計にすべきか，
980円のアナログ時計にすべきか5分間ほど悩んだ挙句，
「安くても時計の機能が不十分なディジタルより高いけどアナログ」
という結論に達して買ったものだ．

そう，時計としての機能の観点ではディジタルは失格である．
なぜディジタルはだめか．
私のようなアナログ人間にとって
「3桁以上の数字を読む」というのは苦痛である．
その点，アナログ時計は直感的に時刻がわかる．

さらに，文字盤は数字1から12が書いていなければならない．
ローマ数字や，単なる12個の印では，何がなんだかわからない．
この数字によって，運転中でも一瞬で時刻を読み取れるわけだ．
車のダッシュボードにもディジタル時計があるが，
それで時刻がわかるのはラジオの時報が鳴ったときだ．

さて，4年前に買った時計，バンドの革の部分がボロボロになったので，
バンドだけ買い換えようとホームセンターへ行くと，

一番安い革のバンドはなんと1500円もする！！！
しかしやはり新品が980円で並んでいたので，
今回もこの厳しい選択基準により，結局以前のものと同じブランドの
ものを買うことになった．4年も経つとデザインもかなりよくなっていて，
その点も満足であった．

めでたしめでたし．

安いだけなら今，ディジタル時計が100円ショップでも売ってる．
でもアナログ時計はないんだな．

さて，最も正確な時計とは，どんな時計だろう．
現在，最も正確なのはセシウム原子時計といわれている．
でも，止まってる時計のほうが正確だもんね．
だって，12時間に1度，真の時刻を指しているに違いないから．
そう，12時間刻みの時計と考えれば，これほど正確な時計はない．

満足！

1999年10月18日月曜日

数学基礎論講義

という本にはまっている．（田中一之　他著　日本評論社）

一応，この分野は自分の専門だから，比較的楽に読める本なのだが，
ちょいと今まで読んだ本とは毛色が違って楽しい本だ．

「はじめに」の中の一文には

「専門家を目指すならこの程度の知識は宴会で酔っぱらってもそれんじられるくらいにマスターしておきたい．」

なんて書いてあるし，ある問題では，

「30分以内に解ければ有段者」

との但し書きがついていたりする．

最近の専門書は昔のように，「木で鼻をくくる」ようなものは少なくなってきた．
高木貞治の「解析概論」が名著といわれるのは
自由で自然な発想で書かれているからでなないかと思う．
（逆に独り言のような書き方で，私はきらいだ）

「木で鼻をくくる」数学書が増えたのは1960年代の「数学の現代化」の
おかげで，このころはブルバキ流の書き方がはやったのだと思う．
数学基礎論という分野はもっともブルバキ流の書き方が似合う分野だから，
この本のような楽しい本はなかなかなかったと思う．

でも，洋書は昔から読み手思いで，師匠からもらった
S.Kleene Introduction to MetaMathematics はとても読みやすかった．

1999年10月16日土曜日

いそがし

ゆうべは徹夜で授業プリントを20ページ分作ろうと思っていたのに，夜8時に学校にノートを忘れたことに気づき，学校へとりに行った．
うちは定時制があるから9時過ぎまであいている．
そんで朝3時までかかって，プリント p.210から p.225 までを仕上げ，
今日，p.201-p.220 まで20ページ分を印刷して配布．
月曜日まで，p.240 まで仕上げて印刷しなければならない．
もう自転車操業だ．

それから，昨日プリントアウトした学力テストの解答例を学年全員分，理系220枚，文系160枚印刷した．ふぅ．

来週火曜日は午後からフェンシングの顧問会議で出張．午後のクラスは自習だよ．

1999年10月15日金曜日

交通ルールを守ろう

どうも，ちかごろ自分は交通ルールを守っていない．
マナーはかなりいいほうだと思うし，基本的に安全運転で，
「無事故」ならかなりの長期間なので保険料の無事故割引も最大だ．
ところが例えば，信号無視は確信犯だ．赤信号はもちろん止まる．
でも，自分の住む田舎道の赤信号では
しばしば自分1台だけがむなしく止まっていることがよくある．
すると必ず，徐行して通過してしまう．
青信号に突っ込んでくるやつもいるから安全確認は十分する．

べつに急いでいるわけではないんだが．
一方通行の逆走とかも，やってしまうんだな．
だからいつまでたってもゴールド免許にはならない．
一時期は「あと1点で免許停止です」なんてハガキまで来た．
道路標識１本分くらいは反則金支払ったかな．

数年前に朝つかまって，遅刻した．
青切符に勤務先を書くとおまわりさん，
「職場には連絡行きませんから」
と気を遣ってくれたけど，気遣いをよそに，
さっそく青切符と反則金の領収書を，教室掲示してしまった．
だって生徒が「先生どうして今日は遅刻したの？」なんてきくんだもん．
正直者のぼくがうそをつけるわけがない．
もちろん「交通ルールを守ろう！」と大書きした紙に張り，
悪い見本（つまり反面教師）として．
生徒はこんなもの見たことないだろうから，勉強になっただろうな．

その日の授業．
「法律違反は本当は罰金か懲役．で，それを決定するのが裁判．
そして罰金刑以上が決定すれば前科になる．
ところが軽い道路交通法違反は，それを認めて反則金を支払うと
裁判を省略してくれるし前科にならないんだよ．青切符をよく見ると書いてあるぞ．
だから反則金制度のない自転車の交通違反は，例えば二人乗りとか一時停止違反とか
検挙されたら本当なら裁判で罰金刑となり，前科１犯ということだけど，
殺傷力は自動車よりかなり少ないのに，自動車よりペナルティーが重いのは
不公平だから，警告で済ましてくれるんだ．
でも自転車や歩行者は相手が悪くても怪我をするのは自分だということを
わすれないでおくれ．」

青切符が役に立った．

1999年10月14日木曜日

バーチャルリアリティ

養老孟司先生が言ってました．

都市というものは古代からバーチャルリアリティの世界．
最近のコンピュータなどの機械の発達で，
バーチャルリアリティが注目されてきただけである．

納得．
庭の中に自然を作りこんだり，
何かをモチーフに建物などをデザインしたりというのは
まさにバーチャルな世界．
都市というのはその存在自体がバーチャルリアリティ．

そういうふうに思えば都市における人間関係の希薄さなどは，
はじめからあったのだ．

1999年10月13日水曜日

バッジョ

すごいすごいすごい
かっこいいなぁ．

1999年10月11日月曜日

高校損得進学率90％以上

同僚のＨ氏との先日の会話の結論．

「まじめに考えれば考えるほど，高校はあほらしい．
高校に見切りをつけて退学する子は，大変正しくまじめな子だ．」

だいたい今時，高校にしがみついてるのは，まじめだからじゃなくて，損得を考えた結果だ．
「高校ぐらい卒業しておかないと…」
と親や先生に損得で説得され，納得させられ，その気になって学校に来ているわけだ．

損得で通っているんだから，適当に力を抜いて，卒業さえしてしまえばいいわけだ．
なるほど，無気力な生徒を見ていると，損得で来ているのだなと思う．

それに応えるべく，われわれ教員は，出席さえしていれば，学力0でも単位を与え，卒業証書を与えるのが仕事になっている．
学力保証はそっちのけだ．
学力を保証しようと力めば力むほど，損得で来ている生徒には煙たがられ，嫌われる．
「もっと気楽にやらせてくれよ」
これは教育困難校だけの問題ではない．
進学校でも受験に関係のない教科科目には見向きもしなくなる生徒が多くなることでもわかる．

入試を廃止して，履歴書に学歴を書くことを禁止したり，会社が学歴によらず学力試験だけで選抜を始めたら，本当に学力を身につけたいまじめな子が学校に戻ってくるかな．

でも，少数だが損得ではなくまじめに考えて高校に通っている子もいて，
彼らのおかげで，私も学校が楽しい．
多くを期待しすぎるのが，大人のよくないところ．
半分以上の生徒が授業を聞いていなくても，よく考えれば半分近くの生徒が授業を聞いてくれていることになる．
まだまだ，捨てたものではないな．

1999年10月10日日曜日

サイエンティフィック・リテラシー

の岩波新書がある．

まだ読んでいない．

現代人のサイエンティフィック・リテラシーの薄っぺらさが，先日の臨界被曝事故と無関係ではなさそうな気がしてならない．
一定質量以上のウランを集めると臨界に達することぐらいは，原子力産業に携わるものにとっては常識だと思っていたが，そうではないらしい．
それとも，扱っている物質がウランであるとは知らされていなかったのだろうか．
これから責任者の「保身」がみられるぞ．
あぁ無責任体質．

私が事件を知ったのは当日の夕方，ラジオの報道で知ったが，
「臨界に達する事故」という報道だった．
臨界という言葉の報道で，自体の重大さを理解したひとはどれくらいいただろう．
私は思わず車をとめて，風向きを確かめてしまったし，その後の天気予報はかなり注意していた．

臨界とは本来原子炉内部でだけ起こしてよいもの．
原爆はまさに臨界そのもの．
現在の核実験は「臨界前核実験」といって臨界にはしない．
それほど臨界は危険なもの．

サイエンティフィック・リテラシーの低下は危険なものに鈍感になり平気で危険なことをしたり，安全なものに必要以上に神経質になり，パニックになったりする．
さらに，科学を悪用されても見抜けない．

これは科学を使って詐欺をはたらいたりすることを指しているわけではない．
大企業や政府といった権力が民衆の収奪に使うということ．
これを助長するのが，科学に対する無知と，他者への無関心．
科学無知ならそもそも巨悪は見抜けないし，科学を知っていても無関心なら見て見ぬ振りをするだろう．
さらに心有る科学者がそれを見抜いても，科学的無知な社会（特にマスコミ）はそれを無視する．
で，気が付くととんでもないことになってるわけだ．

したがって，一般の人も科学の便利さを享受するだけではなく，少しずつでも知識を身に付ける必要もある．
科学に携わるものは他者へ無関心であってはならないし，
ましてや一部のものの利益のために科学を悪用してはならない．
高校で教わるくらいのことは常識だと思うのだが．

ところが科学の基礎知識を教える学校がその機能を果たしてはいない．
それどころか「理科離れが深刻」なんてことになってる．
日本碍子のＣＭ「関係ないじゃん」がまさにそれを表している．
もちろん，これだけ高度にシステム化した社会で，学校の授業内容が直接，巨大システムの説明にはつながらないわけだが．
教員は「教科書を教える」ことに徹し，「教科書の暗記力」を試すテストをする．
ほんとは「教科書で教え」応用力をテストするんだが．
それをやると受験に直結しないから大部分は寝てしまう．
さらに，受験に関係のない学校なら，見向きもしない．
末期的とはこのことだ．

といいながら先日「暗記力テスト（学力テスト）」をやったのだが．

1999年10月8日金曜日

採点

おとといの学力テストの採点をしなければならんのだが，こんなことばかりでさっぱり進まん．
授業のプリントを作成せねばならんし，時給20円でだれか採点してくれないかな．

1999年7月21日水曜日

放物線の長さ

アクセスログによると「放物線の長さ」で検索して，テスト回答にたどり着く人がけっこういる．

きっと，放物線の長さを，計算しようとして行き詰まった人が，ネットで検索したのかな？

それとも，先生から「面白いからためしに計算してみなさい」と課題でも出されたけれどできなくて探したのかな？

まぁ，根性で計算すれば高校の知識で求められる問題ではある．

残念ながら，解答ページには放物線の長さの計算はないので，がっかりしたことでしょう．

ということで，このページに書いてしまおうと思ったけど，人の答えをネットでお気楽に見つけて「課題をやりました」，あるいは「わかったつもり」というのでは，勉強にならない．

苦労してもらいましょう．

解答をフリーの組版ソフト TeX(テフ) で組みました．その TeX のソースをこのページの最後にそのまま置きました．

私の解答を手に入れる方法をここに書きます．

ソースを自分でタイプセットする．（なければ自分のマシンに LaTeX をインストールしよう）
TeX がなくインストールする根性もなければ，ソースはプレーンのテキストだからソースを解読する．
私に質問をして聞き出す．
私はタイプセットしたものをpdfで持っています．苦労や努力が嫌いで自力でやるのがいやな人は，「ファイルをください」とメールする．

2003年12月3日追記

2003年12月3日に，千里国際学園のB先生からいただいたメールでの指摘に基づき，いくつかの本文中の記号などのミスを訂正し，訂正では書ききれない部分を最後に追記した．

2003年12月4日追記

逆双曲正弦関数 Arcsinh x は Log で書けるのでした．

\begin{verbatim}
以下TeXソース

\documentclass{jarticle}

\title{放物線の長さ}
\author{くろべえ}
\date{1999年10月}
\西暦

\begin{document}
\maketitle

放物線の長さを求める問題は，高校の範囲でできるとはいえ，結構厄介である．
ここでは $y=x^2$ の区間 $[0,\ 1]$ における長さを求めてみる．

$y=f(x)$ の区間 $[a,\ b]$ における長さは，
高校の教科書によれば
\begin{quote}
$\displaystyle\int_a^b\sqrt{1+(f^\prime (x))^2}\,dx$
\end{quote}
で与えられる．

$f(x)=x^2$ とすれば $f^\prime (x)=2x$ より，区間 $[0,\ 1]$ における長さは，
$\displaystyle\int_0^1\sqrt{1+(2x)^2}\,dx$ で与えられる．

\begin{quote}
$\displaystyle
\int_0^1\sqrt{1+(2x)^2}\,dx \\
= \int_0^1\sqrt{1+4x^2}\,dx
$.
\end{quote}
ここで，$2x=\tan\theta$ とおけば $4x^2=\tan^2\theta$ で，
積分区間は$x$ が $[0,\ 1]$ だったので，
$\theta$ は$\tan \alpha=2$ に対して $[0,\ \alpha] $ となり，
$dx=\frac{1}{2\cos^2\theta}\,d\theta$ より，
\begin{quote}
$\displaystyle
\int_0^1\sqrt{1+4x^2}\,dx \\
=\int_0^\alpha
\sqrt{1+\tan^2\theta}\frac{1}{\cos^2\theta}\,d\theta \\
=\int_0^\alpha
\sqrt{\frac{1}{\cos^2\theta}}\frac{1}{2\cos^2\theta}\,d\theta \\
=\frac{1}{2}
\int_0^\alpha
\frac{1}{\cos\theta}\frac{1}{\cos^2\theta}\,d\theta \\
=\frac{1}{2}
\int_0^\alpha
\frac{1}{\cos^3\theta}\,d\theta \\
=\frac{1}{2}
\int_0^\alpha
\frac{\cos\theta}{\cos^4\theta}\,d\theta \\
=\frac{1}{2}
\int_0^\alpha
\frac{\cos\theta}{(\cos^2\theta)^2}\,d\theta \\
=\frac{1}{2}
\int_0^\alpha
\frac{\cos\theta}{(1-\sin^2\theta)^2}\,d\theta
$.
\end{quote}
ここで，$\sin\theta=u$ とおけば $\cos\theta\,d\theta=du$ で，
$\theta$ の積分区間は $\tan \alpha=2$ に対して $[0,\ \alpha]$ だったので，
$\sin\alpha=\sqrt{1-\cos^2\alpha}=\sqrt{1-\frac{1}{1+\tan^2\alpha}}
\sqrt{1-\frac{1}{1+2^2}}=\sqrt{\frac{4}{5}}=\frac{2}{\sqrt{5}}$ より，
$u$ の積分区間は $[0,\ \frac{2}{\sqrt{5}}] $ となり，
\begin{quote}
$\displaystyle
\frac{1}{2}
\int_0^\alpha
\frac{\cos\theta}{(1-\sin^2\theta)^2}\,d\theta \\
=\frac{1}{2}
\int_0^\frac{2}{\sqrt{5}}
\frac{1}{(1-u^2)^2}\,du \\
$
\end{quote}
$\frac{1}{(1-u)^2(1+u)^2}$ を部分分数に分解する．
\begin{quote}
$\displaystyle
\frac{1}{(1-u)^2(1+u)^2}
=\frac{a}{1-u}
+\frac{b}{(1-u)^2}
+\frac{c}{1+u}
+\frac{d}{(1+u)^2}
$
\end{quote}
とおき，両辺に $(1-u^2)^2$ をかけて分母を払うと
\begin{quote}
$\displaystyle
1 = a(1-u)(1+u)^2+b(1+u)^2+c(1-u)^2(1+u)+d(1-u)^2 \\
1 = (-a+c)u^3+(-a+b-c+d)u^2+(a+2b-c-2d)u+(a+b+c+d)
$
\end{quote}
これは恒等式だから（要するに左辺を $0u^3+0u^2+0u+1$ と考え係数を合わせて）
\begin{quote}
$\displaystyle
-a+c=0,\\
-a+b-c+d=0,\\
a+2b-c-2d=0,\\
a+b+c+d=1.
$
\end{quote}
この連立方程式を解くと，$a=b=c=d=\frac{1}{4}$ より
\begin{quote}
$\displaystyle
\frac{1}{2}
\int_0^\frac{2}{\sqrt{5}}
\frac{1}{(1-u^2)^2}\,du \\
=\frac{1}{2}\cdot\frac{1}{4}
\int_0^\frac{2}{\sqrt{5}}
\left(
\frac{1}{1-u}
+ \frac{1}{(1-u)^2}
+ \frac{1}{1+u}
+ \frac{1}{(1+u)^2}
\right)\,du
\\
=\frac{1}{8}
\left[
-\log(1-u)+\frac{1}{1-u}+\log(1+u)+\frac{-1}{1+u}
\right]_0^\frac{2}{\sqrt{5}}
\\
=\frac{1}{8}
\left(
-\log\left(
1-\frac{2}{\sqrt{5}}
\right)
+\frac{1}{1-\frac{2}{\sqrt{5}}}
+\log\left(
1+\frac{2}{\sqrt{5}}
\right)
+\frac{-1}{1+\frac{2}{\sqrt{5}}}
\right)
\\
=\frac{1}{8}\left(
-\log\left(
1-\frac{2}{\sqrt{5}}
\right)
+\frac{1}{1-\frac{2}{\sqrt{5}}}
+\log\left(
1+\frac{2}{\sqrt{5}}
\right)
+\frac{-1}{1+\frac{2}{\sqrt{5}}}
\right)\\
=\frac{4\sqrt{5}+\log\frac{5+2\sqrt{5}}{5-2\sqrt{5}}}{8}
$
\end{quote}
約 1.47894 である．

ついでに原始関数を求めて見よう．
結局，上記の積分の計算から，
\begin{quote}
$\displaystyle
\frac{1}{8}\left(
-\log\left(1-u\right)
+\frac{1}{1-u}
+\log\left(1+u\right)
+\frac{-1}{1+u}
\right)\\
=\frac{1}{8}\left(
\frac{2u}{1-u^2}
+\log\frac{1+u}{1-u}
\right)\\
$
\end{quote}
となることまではわかる．$u=\sin\theta$ より，
\begin{quote}
$\displaystyle
\frac{1}{8}\left(
\frac{2u}{1-u^2}
+\log\frac{1+u}{1-u}
\right)\\
=\frac{1}{8}\left(
\frac{2\sin\theta}{1-\sin^2\theta}
+\log\frac{1+\sin\theta}{1-\sin\theta}
\right)\\
$
\end{quote}
とりあえず，$\frac{2\sin\theta}{1-\sin^2\theta}$
の部分は
\begin{quote}
$\displaystyle
\frac{2\sin\theta}{1-\sin^2\theta}\\
=\frac{2\sqrt{1-\cos^2\theta}}{\cos^2\theta} \\
=\frac{2\sqrt{1-\frac{1}{1+\tan^2\theta}}}{\frac{1}{1+\tan^2\theta}} \\
=\frac{2\sqrt{1-\frac{1}{1+(2x)^2}}}{\frac{1}{1+(2x)^2}} \\
=2(1+4x^2)\sqrt{\frac{4x^2}{1+4x^2}} \\
=2(1+4x^2)\frac{2x}{\sqrt{1+4x^2}} \\
=4x\sqrt{1+4x^2} \\
$
\end{quote}
と，$x$ の関数で表せるが，
$\log\frac{1+\sin\theta}{1-\sin\theta}$ の部分はまず無理のような気がする．
Mathematica で計算させたら
ArcSinh[2x] と，高校数学では出てこない関数で表現された．

\begin{quote}
$\displaystyle
\frac{1}{8}\left(
\frac{2\sin\theta}{1-\sin^2\theta}
-\log\frac{1+\sin\theta}{1-\sin\theta}
\right)\\
=\frac{1}{8}\left(
\frac{2\sin\theta}{\cos^2\theta}
-\log\frac{1+\sin\theta}{1-\sin\theta}
\right)\\
$
\end{quote}
を微分する問題をテストで出したことがあった．
微分は，何の工夫もないただの計算問題である．

\vspace{\baselineskip}
\textbf{\large 2003年12月3日追記}
\vspace{\baselineskip}

2003年12月3日に，千里国際学園のB先生からいただいたメールでの
指摘に基づき，
いくつかの本文中の記号などのミスを訂正しました．

さらに，本文の
\begin{quote}
「$\log\frac{1+\sin\theta}{1-\sin\theta}$ の部分はまず無理のような気がする．
」
\end{quote}
という部分に対しても，次のような指摘がありました．

\begin{quotation}
一番前の$\frac{1}{8}$
を$\frac{1}{4}$にして中に$\frac{1}{2}$を掛けると、
$\log$の中が$\sqrt{\frac{1+\sin\theta}{1-\sin\theta}}$となり、
これを変形すれば、
$\log$の中は$\sec\theta+\tan\theta$となって、
結局求める不定積分は
$\frac{1}{4}\left(2x\sqrt{1+4x^2}+\log(2x+\sqrt{1+4x^2}\right)+C$
となります。

また、赤チャートの「44無理関数の積分法」のページには別解が掲載されてます。
すでにご存知でしたら失礼をお許し下さい。

\end{quotation}

つまり，
$\log\frac{1+\sin\theta}{1-\sin\theta}
=\log\frac{(1+\sin\theta)^2}{(1-\sin\theta)(1+\sin\theta)}
=\log\frac{(1+\sin\theta)^2}{1-\sin^2\theta}
=\log\frac{(1+\sin\theta)^2}{\cos^2\theta}
=2\log\frac{1+\sin\theta}{\cos\theta}
=2\log\left(\frac{1}{\cos\theta}+\frac{\sin\theta}{\cos\theta}\right)
=2\log\left(\sqrt{\frac{1}{\cos^2\theta}}+\tan\theta\right) \\
=2\log\left(\sqrt{1+\tan^2\theta}+\tan\theta\right)
=2\log\left(\sqrt{1+(2x)^2}+2x\right)
$ と $x$ の式に変形できる．

さらに，数研出版の赤チャートの「44無理関数の積分法」のページには
$\int\sqrt{x^2+a^2}\, dx$ が解説されており，
そこでは$x+\sqrt{x^2+a^2}=t$ とおいて，
$x^2+a^2=(t-x)^2$, $2tx=t^2-a^2$,
$x=\frac{1}{2}\left(t-\frac{a^2}{t}\right)$,
$dx=\frac{1}{2}\left(1+\frac{a^2}{t^2}\right)dt$ と
置換することにより，
三角関数に置換することなく
簡単に導く方法が示されている．

実際，この放物線の長さの問題の場合は，
$2x+\sqrt{1+4x^2}=t$ とおけば，あとは同じである．

私自身は浅学非才で，赤チャートのこの部分は知らなかった．

\vspace{\baselineskip}
\textbf{\large ArcSinh[x]について．}
\vspace{\baselineskip}

本文では「高校数学では出てこない関数で表現された」と書いたが，
これは $\sinh x = \frac{e^{x}-e^{-x}}{2}$ の逆関数なので，
初等関数で表すことができ，
実際 $\log\left(\sqrt{1+x^2}+x\right)$
となる．

\begin{quote}
$y=\sinh^{-1} x$ ならば
$x = \sinh y = \frac{e^{y}-e^{-y}}{2}$, より，
$2x = e^{y}-\frac{1}{e^{y}}$,

両辺を $e^y$倍して
$2xe^y = e^{2y}-1$,

$e^y$ で整理すると $e^y$ の2次方程式となって，
$ (e^{y})^2-2xe^y-1 =0$,

$e^y=x+\sqrt{x^2-(-1)}=x+\sqrt{x^2+1}$,

したがって，
$y=\log(x+\sqrt{x^2+1})$ となる．
\end{quote}

つまり Mathematica が表示した
Arcsinh[2x] は初等関数で\\
$\log(2x+\sqrt{4x^2+1})$ と表されたのである．

赤チャートの置換は逆$\sinh x =\log(x+\sqrt{x^2+a^2})$
で $e^y = t$ に置換したといえる．

\end{document}

1999年7月10日土曜日

1999年1学期一斉テスト

1999年7月に3年生に実施したいわゆる期末テスト。
＞ PDF と TeXソース
卒業生（浪人中）のNくんは，「去年授業でよい成績とれずに悔しかったからテストを受けさせてほしい」ということで，このテスト問題に挑戦した．

数学III１学期一斉テスト

(100分)配点は生徒の出来による．
つまり正解者が少ないほどオッズがあがり，配点も大きくなる．
この方法だと，121人受験した場合，全員正解の問題と，
一人のみ正解の問題では最大で，121倍のオッズの比になるが，
それを3倍に補正してから，100点満点に配分している．
問題ごとにオッズと配点を記した．

平均23．8，標準偏差12．1
N君は得点55点．したがって偏差値76．

$\frac{5}{3}$は第何象限の角か．

N君の答

第2象限

解答

5/3=1.666... は π/2=1.57... より大きく、 π=3.14... より小さいので、第2象限である。

解説

弧度法（ラジアン）に慣れていくと、πが単位のように思えてくる。すると、「πが抜けている。印刷ミスでは？」といいたくなる。これはそういう人に対する引っかけ問題である。 πは単位でもなんでもなく、定数 3.14… である。

結果

○ 66人 △ 0人 × 55人オッズ 1.8 配点 2.99 ×の大多数が、5π/3 と勘違いして、第4象限と答えている。

数列 $\{n\sin\frac{a}{n}\}$ （$a$は定数）の極限を求めよ．

N君の答

解答

$n\sin\frac{a}{n}=\frac{\sin\frac{a}{n}}{\frac{1}{n}}=a\frac{\sin\frac{a}{n}}{\frac{a}{n}}\stackrel{n\to\infty}{\longrightarrow}a\cdot 1=1$

解説

基礎的な問題、単純な式変形で、 x->0 なら sin x / x -> 1 の形に持ち込む。

結果

○ 41人 △ 0人 × 80人

オッズ 3.0 配点 3.42

$\lim_{x\to 0}\frac{1-\cos ax}{x^2}$ （$a$は定数）を求めよ．

N君の答

a^2/2

解答

　　　$\frac{1-\cos ax}{x^2}=\frac{(1-\cos ax)(1+\cos ax)}{x^2(1+\cos ax)}\\=\frac{1-\cos^2 ax}{x^2(1+\cos ax)}=\frac{\sin^2 ax}{x^2}\cdot\frac{1}{1+\cos ax}\\=\frac{\sin^2 ax}{(ax)^2}\cdot\frac{a^2}{1+\cos ax}=\left(\frac{\sin ax}{ax}\right)^2\cdot\frac{a^2}{1+\cos ax}\\\stackrel{x\to0}{\longrightarrow}1^2 \cdot\frac{a^2}{1+\cos 0}=\frac{a^2}{2}$

解説

前問よりちょいとひねりが加えられているが、式変形で、 x→0 なら sin x / x → 1 の形に持ち込む。

結果

○ 40人 △ 0人 × 81人オッズ 3.0 配点 3.44

$\lim_{x\to 0}\displaystyle\frac{\log\cos x}{x^2}$ を求めよ．

N君の答

-1/2

解答

$\frac{\log\cos x}{x^2}=\frac{1}{x^2} \log(1-\sin^2 x)^{\frac{1}{2}}=\frac{1}{x^2}\cdot\frac{1}{2} \log(1-\sin^2 x)\\=\frac{1}{2x^2}\log\left( (1-\sin^2 x)^{\frac{1}{-\sin^2 x}}\right)^{-\sin^2 x}\\=\frac{-\sin^2 x}{2x^2}\log\left(1+(-\sin^2x)\right)^{\frac{1}{-\sin^2 x}}\\=\frac{-1}{2}(\frac{\sin x}{x})^2\log(1+(-\sin^2x))^{\frac{1}{-\sin^2 x}}\\\stackrel{x\to0}{\longrightarrow}\frac{-1}{2}\cdot1^2\cdot\log e=\frac{-1}{2}$

解説

今度は log がらみ。やはり式変形で　 x→0 なら sin x / x → 1, (1+x)^(1/x) → e の形に持ち込む。

結果

○ 8人 △ 0人 × 113人オッズ 15.1 配点 5.43 さすがに複合問題は難しい。

$\frac{1}{4}\log\displaystyle\frac{1+\sin x}{1-\sin x}+\displaystyle\frac{\tan x}{2\cos x}$を微分せよ．

N君の答

無回答

放物線の長さ

解答

$\left(\log\displaystyle\frac{1+\sin x}{1-\sin x}+\displaystyle\frac{\tan x}{2\cos x}\right)'=\frac{1}{\cos^3 x}$

解説

とても詳細を書く気がしない。答え 1/cos^3 x を積分して作った問題である。「10桁の掛け算をやれ」といってるような問題で、工夫もなにもなく、ただひたすら計算するのみ。大量の計算を、見失うことなく自分なりに整理して正確に実行する力が求められる。もちろん、この答えを積分して、問題の式を導くのは10倍難しい。

結果

○ 25人 △ 0人 × 96人オッズ 4.8 配点 3.93 25人もできた。あたりまえか。

級数 $\sum_{n=0}^{\infty}\left(\displaystyle\frac{x}{2}\right)^{n+1}$ について，

(1)級数が収束するための $x$ の範囲を求めよ．
(2)そのときの和を求めよ．

N君の答

0≦x≦2

x^2/(4-2x)

解答

解説

教科書レベルのやさしい問題。ただ、n=0 からはじまってるところがひっかけといえば、ひっかけである。

結果(1)

○ 49人 △ 0人 × 72人オッズ 2.5 配点 3.25

結果(2)

○ 20人 △ 0人 × 101人オッズ 6.1 配点 4.19

　$x=\sin y$ (ただし，$-\frac{\pi}{2}\le y\le\frac{\pi}{2}$)のとき，

(1) $\frac{dy}{dx}$を $x$の式で表せ．
(2) $\frac{d^2y}{dx^2}$を求めよ．

N君の答

1/√(1-x^2)

x(1-x-2)^(3/2)

解答

(1) $\frac{dy}{dx}=\frac{1}{\frac{dx}{dy}}=\frac{1}{\cos y}=\frac{1}{\sqrt{1-\sin^2 y}}=\frac{1}{\sqrt{1-x^2}}$

(2) $\frac{d^2y}{dx^2}=\left(\frac{1}{\sqrt{1-x^2}}\right)'=\left((1-x^2)^{\frac{-1}{2}}\right)'\\=\frac{-1}{2}(1-x^2)^{\frac{-3}{2}}(-2x)=\frac{x}{(1-x^2)\sqrt{1-x^2}}$

解説

教科書章末問題レベルの基礎的な問題。解答の中に書かなかったが、平方根が正のみであるのは、y の範囲からいえる。問題文の但し書きは飾りじゃないのよ。

結果(1)

○ 35人 △ 0人 × 86人オッズ 3.5 配点 3.57

結果(2)

○ 12人 △ 0人 × 109人オッズ 10.1 配点4.84

$\lim_{x\to0}\frac{a^x-1}{x}$を求めよ．

N君の答

解答

$t=a^x-1 \Rightarrow x=\log_{a}(1+t)\\x\to0\Rightarrow t\to0\\\frac{a^x-1}{x}=\frac{t}{\log_{a}(1+t)}=\frac{1}{t}\log_{a}(1+t)=\frac{1}{\log_{a}(1+t)^{\frac{1}{t}}}\\\to\frac{1}{\log_{a}e}=\log a$

解説

極限の問題なので、解答例の解き方が正統なのだろうが、記述式ではなく、解答欄を埋めるだけなのだから、微分の公式を使って、$f(x)=a^x,\ f'(x)=a^x\log a$
$\frac{a^x-1}{x}=\frac{a^x-a^0}{x-0}=\frac{f(x)-f(0)}{x-0}\\\stackrel{t\to0}{\longrightarrow}f'(0)=a^0\log a=1\log a=\log a$

とすると簡単である。

結果

○ 14人 △ 0人 × 107人オッズ 8.6 配点 4.63

$y=\frac{a}{2}\left(e^{\frac{x}{a}}+e^{\frac{-x}{a}}\right)$のとき，

(1) $y''$を $y$で表せ．
(2)$y^{(2n)}$ を $y$で表せ．

N君の答

y/a^2

(1/a^2)y or y^(2n)

解答

(1) $y'=\frac{a}{2}\left((e^{\frac{x}{a}})'+(e^{\frac{-x}{a}})'\right)=\frac{a}{2}\left(\frac{1}{a}e^{\frac{x}{a}}+\frac{-1}{a}e^{\frac{-x}{a}}\right)=\frac{1}{2}\left(e^{\frac{x}{a}}-e^{\frac{-x}{a}}\right)$
$y''=\frac{1}{2}\left((e^{\frac{x}{a}})'-(e^{\frac{-x}{a}})'\right)=\frac{1}{2}\left(\frac{1}{a}e^{\frac{x}{a}}-\frac{-1}{a}e^{\frac{-x}{a}}\right)\\=\frac{1}{2a}\left(e^{\frac{x}{a}}+e^{\frac{-x}{a}}\right)=\frac{1}{a^2}\frac{a}{2}\left(e^{\frac{x}{a}}+e^{\frac{-x}{a}}\right)=\frac{1}{a^2}y$

(2) 記述式答案なら例えば次のように書くことも考えられる。数列$\{y^{(2n)}\}$は，$y^{2(n+1)}=y^{2+2n}=(y'')^{(2n)}=\left(\frac{1}{a^2}y\right)^{(2n)}=\frac{1}{a^2}y^{(2n)}$
より初項 $y^{(2\cdot 1)}=y''=\frac{1}{a^2}y$，公比$\frac{1}{a^2}$の等比数列で，$y^{(2n)}=\frac{1}{a^{2n}y$．

しかし、一番手堅いのは 4階微分, 6階微分を求めて 2n 階微分を類推し、数学的帰納法で証明することかな。

解説

結果(1)

○ 40人 △ 0人 × 81人オッズ 3.0 配点 3.44

結果(2)

○ 21人 △ 0人 × 100人オッズ 5.8 配点 4.13 以上解答欄に答えを書くだけの問題だから、答えが合っていれば、どんな解き方をしても正解である。
しかし、以下の問題は答案に不備があれば、答えが合っていても減点される記述式。

数列 $\{\sin\sqrt{n+1}-\sin\sqrt{n}\}$ の極限を求めよ．

N君の答

無解答．平均値の定理を使う基礎的な問題だぞ．

解答

$\sin\sqrt{n+1}-\sin\sqrt{n}=2\cos\frac{\sqrt{n+1}+\sqrt{n}}{2}\sin\frac{\sqrt{n+1}-\sqrt{n}}{2}$
$\sqrt{n+1}-\sqrt{n}=\frac{(\sqrt{n+1}-\sqrt{n})(\sqrt{n+1}+\sqrt{n})}{\sqrt{n+1}+\sqrt{n}}=\frac{n+1-n}{\sqrt{n+1}+\sqrt{n}}\\=\frac{1}{\sqrt{n+1}+\sqrt{n}}\to0$
より$\sin\frac{\sqrt{n+1}-\sqrt{n}}{2}\to0$
$\cos\frac{\sqrt{n+1}+\sqrt{n}}{2}$は有界(-1以上1以下)だから
$\cos\frac{\sqrt{n+1}+\sqrt{n}}{2}\sin\frac{\sqrt{n+1}-\sqrt{n}}{2}\to0$　より　$\sin\sqrt{n+1}-\sin\sqrt{n}\to0$

解説

cos の有界と sin の無限小両方に言及して満点。片方で得点半分。この問題は今回の試験範囲ではない微分の応用「平均値の定理」を使うとすぐできる問題であるが、三角関数の公式でできる問題なので、出題した。予習が進んでいると思われる2名の生徒が「平均値の定理」を使用して解いた。もちろん正解である。

結果

○ 1人 △ 8人 × 112人オッズ 24.2 配点 6.20

級数　$1+\frac{1}{2^2}+\frac{1}{3^2}+\ \cdots\ +\frac{1}{n^2}+\ \cdots$ 　について次の問いに答えよ．

解説

結果

○ 1人 △ 8人 × 112人オッズ 24.2 配点 6.20

級数　$1+\frac{1}{2^2}+\frac{1}{3^2}+\ \cdots\ +\frac{1}{n^2}+\ \cdots$ 　について次の問いに答えよ．

N君の答

無解答．平均値の定理を使う基礎的な問題だぞ．

解答

(1) 部分和が単調増加であることを示せ．

N君の答

1+1/2^2+1/3^2+1/n^2=S(n) とおくと，S(n)-S(n-1)=1/n^2＞0

解答

N君の答えで正解．

解説

まぁ，「級数の各項が正の数だから単調増加」でもOK でしょう．

結果

○ 39人 △ 3人 × 79人オッズ 3.0 配点 3.43 (2) 部分和は有界であることを示せ．(Hint $n^2>n(n-1)$をうまく使う)

N君の答

1/n(n-1) ＞ 1/n^2 k≧2 のとき，

n
∑ 1/k(k-1) ＞
k=2

n
∑ 1/k^2
k=2

1-1/n＞1/2^2+1/3^2+…+1/n^2 2-1/n＞1+1/2^2+1/3^2+…+1/n^2 lim 2-1/n =2 ＞ lim 1+1/2^2+1/3^2+…+1/n^2 ∴有限

解答

Hint の両辺の逆数を取ることにより$\frac{1}{n(n-1)}>\frac{1}{n^2}$が成り立つから
$k\ge2$のとき$\sum_{k=2}^{n}\frac{1}{k(k-1)}>\sum_{k=2}^{n}\frac{1}{k^2}$
ここで，$\frac{1}{k-1}-\frac{1}{k}=\frac{k}{k-1}-\frac{k-1}{k(k-1)}=\frac{1}{k(k-1)}$より
$\sum_{k=2}^{n}\frac{1}{k(k-1)}=\frac{1}{1\cdot2}+\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+\frac{1}{4\cdot5}+\ \cdots\ +\frac{1}{(n-1)n}\\=\left(\frac{1}{1}-\frac{1}{2}\right)+\left(\frac{1}{2}-\frac{1}{3}\right)+\left(\frac{1}{3}-\frac{1}{4}\right)+\left(\frac{1}{4}-\frac{1}{5}\right)+\ \cdots\ +\left(\frac{1}{n-1}-\frac{1}{n}\right)\\=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\ \cdots\ +\frac{1}{n-1}-\frac{1}{n}\\=1-\frac{1}{n}$

解説

Hint なしで解ける生徒はその手の問題を経験済みといえる．そんなミラクルテクニックの知識を問うつもりは毛頭ないので，はじめから Hint を与え，「論述能力」を見た．

結果

○ 4人 △ 5人 × 112人オッズ 18.6 配点 5.76
(3) 級数の極限について述べなさい．

N君の答

(2) より 2

解答

単調増加で上に有界な数列は収束する．という定理から (1), (2) により級数は収束する．

解説

極限は 2 以下の数であることが (2) より保証される． N君は2が極限であるとしているが，この定理は極限の存在をアプリオリに保証するだけで，極限値を求める手段は与えない．実際この級数の極限は π^2/6=1.64493…　で，2よりだいぶ小さい．

結果

○ 16人 △ 1人 × 104人オッズ 7.3 配点 4.42

$f(x)$ の $x=a$ における微分係数$f'(a)$ を定義せよ．

N君の答

f '(a)＝

　　　 f(x)-f(a)
lim　―――――
x→a 　 x-a

f '(a)＝

　　　 f(a+h)-f(a)
lim　―――――
h→0 　　h

解答

$\lim_{x\to a}\frac{f(x)-f(a)}{x-a}$が存在するとき，それを$f(x)$の$x=a$における微分係数といい，$f'(a)$と書く．

解説

式だけしか書いていない△が多い．極限の存在が微分の定義である．

結果

○ 2人 △ 57人 × 62人オッズ 4.0 配点 3.71

$\sqrt{x}$ の導関数が $\frac{1}{2\sqrt{x}}$ であることを微分の定義にしたがって示せ．

解説

教科書丸写しの問題．

結果

○ 62人 △ 3人 × 56人オッズ 1.9 配点 3.02

「$f(x)=\left{x^2+1\ (x\ge 1)\\ x^2-1\ (x\lt 1)\right.$
で定義された関数の導関数はx<1>1 のとき2x だから，x→1 のとき2x→2 より， x=1 の微分係数は 2 である．」とするのは間違いである．微分の定義にしたがって，間違いを正せ．

N君の答

微分可能であるということはその点において連続関数であること必要がある．しかしこの関数は x=1 において不連続でありこれは微分できないということになりうる．

解答

f(1)=2 なので，
x>1 のとき f(x)=x^2+1 より
$\lim_{x\to 1+0}\frac{f(x)-f(1)}{x-1}=\lim_{x\to1+0}\frac{x^2+1-2}{x-1}=\lim_{x\to1+0}\frac{x^2-1}{x-1}=\lim_{x\to1+0}\lim\frac{(x-1)(x+1)}{x-1}=\lim_{x\to1+0}(x+1)=2$
x$\lim_{x\to 1-0}\frac{f(x)-f(1)}{x-1}=\lim_{x\to1-0}\frac{x^2-1-2}{x-1}=\lim_{x\to1-0}\frac{(x-1)(x+1)-2}{x-1}=\lim_{x\to1-0}\lim\left(x+1+\frac{-2}{x-1}\right)=+\infty$
よって，$\lim_{x\to1}\frac{f(x)-f(1)}{x-1}$が存在しないので，x=1 の微分係数は存在しない．

解説

定理「微分可能なら連続」があるので，その対偶「不連続なら微分不可能」はいつでもいえる．したがってこの問題は明らかだが，それを「微分の定義」にしたがって，示してはじめて正解である．

結果

○ 2人 △ 2人 × 117人オッズ 40.3 配点 7.16

奇関数の導関数は偶関数であることを証明せよ．あ，もちろん関数は微分可能だからね．

N君の答

f(x) を奇関数とすると， f(x)=-f(-x)．微分すると f '(x)=f '(-x) おっとーこれは偶関数．

解答

f(x) を奇関数とすると， f(x)=-f(-x)．両辺を微分すると f '(x)=-f '(-x)×(-1) = f '(-x)．したがって f '(x) は偶関数．

解説

わかってみればこれだけの問題，ところが出来は悪い．

結果

○ 2人 △ 1人 × 118人オッズ 48.4 配点 7.54 次の問題は最後のふたつ正解者がいなかったので，全員に○を与えた．その上で，9月1日期限の「レポート」とした．

x≠0のとき $f(x)=x^2\sin\frac{1}{x}$，f(0)=0 と定義された関数について次の問いに答えよ。

(1) f(x) が連続かどうか調べよ。

N君の答

x →+0 のとき，f(x)=x^2 sin(1/x)→ +sin∞. x →-0 のとき，f(x)→ -sin∞. よって連続にはならない

解答

_x→0

解説

教科書の連続の定義に当てはまるかどうかを検証するだけである．
教科書では関数の連続をつぎのように定義している．

f(a) が定義されていて
lim_x→a f(x)が存在し，
lim_x→a f(x)＝f(a).

結果

○ 4人 △ 6人 × 111人オッズ 17.3 配点 5.64
(2) x≠0のとき f '(x) を求めよ。

N君の答

f(x)=x^2 sin(1/x) なので， f '(x)=2x sin(1/x) + x^2 (-1/x^2) cos(1/x) =2x sin(1/x) - cos(1/x)

解答

N 君の解答のとおりで問題ない．

解説

これは計算問題，たくさんの人ができた．めでたしめでたし．

結果

○ 43人 △ 1人 × 77人オッズ 2.8 配点 3.36
(3) f' (0) を求めよ。

N君の答

解答

(2) で求めた導関数は当然 x≠0 のときである． f '(0) は定義に従って求めて，極限が存在するときだけ存在する． x→0 のとき (f(x)-f(0))/(x-0) の極限が存在すればそれが f '(0). f(0)=0 より　(f(x)-f(0))/(x-0) ＝ f(x)/x ＝ x sin(1/x). x→0 のとき 1/x は発散するが，sin(1/x) は有界． x は無限小だから x sin(1/x) は無限小．したがって，f '(0)＝0 が存在する．

解説

微分とはあくまで微分の定義の極限が存在するかどうかである．

結果

○ 121人正解者なしのため全員に得点 △ 0人 × 0人オッズ 1 配点 2.51
(4) f '(x)が連続かどうか調べよ。

N君の答

x→+0 のとき f '(x) → 2sin∞-cos∞． x→-0 のとき f '(x) → -2sin∞-cos∞．よって不連続

解答

2x sin(1/x) は無限小であるが， cos(1/x) は振動するから， x→0 のとき f '(x) は振動．しかし，f '(0) が定義されているから f '(x) は x＝0 で不連続．

解説

(2) でもとめた導関数の極限と f '(0) が一致するかどうかである．これも教科書の連続性の定義どおりに考える．

結果

○ 121人正解者なしのため全員に得点 △ 0人 × 0人オッズ 1 配点 2.51

1999年6月25日金曜日

数学III抜き打ちテスト

6月に3年生に実施したテスト。
＞　PDF と TeXソース

内容は，授業の「お話」をどれだけ，自分のものにしているか？というもの．問題を解く力ではなく，「どれだけ数学的概念が言語化されているか」というものを試している．卒業生（浪人中）のNくんは，「去年授業でよい成績とれずに悔しかったからテストを受けさせてほしい」ということで，このテスト問題に挑戦した．私の授業を受けていないぶん，現役生よりハンデはあるが，それなりに言語化されているのはさすが浪人生で，得点も17点で現役生の平均点に近く，偏差値も 49.1 である．

現役生に対しては，テスト後すべて解答をレポートにして提出することを義務付け，その出来によって「満点に足りない得点の半分を挽回する」ということにした．
数学III抜打ちテスト
(50分)12問あるので配点は1問 100/12=8.333
117人受験，平均 18.624 標準偏差 18.49

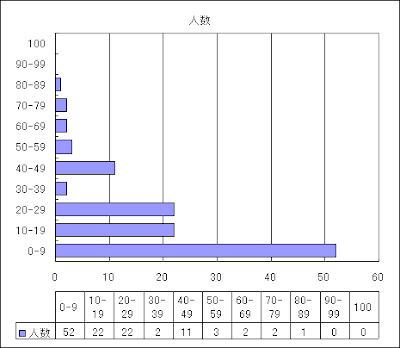
「写像」と「対応」の違いについて説明せよ．

卒業生 N君の答

写像ってのは２つの集合 A, B っていうものがあり， A の内の1つの要素が B の内に1つと組になっていること．対応はなっていない場合，つまり A∋x, A∋y, B∋a について xとa, yとa もOK ということ

N君の解答はなんとなく言おうとしていることはわかるが，正確さには欠けている．数学のテストである以上，ある程度の正確さを要求するため，この解答は0点である．

解答例1

集合 A, B に対し A の要素おのおのについて， B の要素がただひとつ対応するとき，A から B への写像といい，ただひとつに限らないのが対応

高校生ならこの程度で正解とした．

解答例2

集合 A, B の対応とは {(a, b)| a∈A, b∈B} の部分集合，集合 A から B への写像とは「 {(a, b)| a∈A, b∈B}の部分集合で，『(a, x), (a, y) ならば x=y』を満たすもの」

かなりテクニカルな解答．2人の生徒がこのように答えた．よく理解し，記号等の使い方も的確である．

結果

命題「ある区間 (a-p, a+p) をとれば区間内のすべての x について f(x)≦f(a)」の否定命題を述べよ．

卒業生 N君の答

任意の値 x において f(x)＞f(a) が成り立つならば区間 (a-p, a+p) はとらない．

これは授業で論理の言葉「すべての～」，「ある～」を解説した．その使用法の問題である．授業を受けていない N君には無理． ∀（すべて），∃（ある），￢（否定）の記号を使えば，ド・モルガンの法則￢∀x P(x) ⇔ ∃x￢P(x), ￢∃x P(x) ⇔ ∀x￢P(x) が使える使えるかどうかの問題．ちなみにこの命題は「極大」の定義である．（f(a) が極大値．不等号の向きを変えれば極小）そしてその否定命題は「極大でない」ことの表現になる．

解答例

機械的にド・モルガンの法則を適用すれば，すべての区間(a-p, a+p) について区間内のある x について f(x)＞f(a).

もうすこしこなれた言い方をすれば，どんな区間(a-p, a+p) をとっても，区間内にある x が存在して f(x)＞f(a).

結果

有界と無限小を定義せよ．

卒業生 N君の答

有界とはある値を表す方程式 f(x) の x をある値に近づけたとき全てに f(x) が収束する場合，f(x) は有界であるという．無限小とは f(x) の x をある値 a に近づけたとき f(x) が負方向に限りなく小さくなっていく場合 f(a) は無限小という．

これも授業を受けていなければ当然無理．ただし，無限小は「負の無限大」とは違う．いくらでも0に近い状態である．それをいかに言語化するか．

解答例

変数 x が有界とは，ある正の数 M が存在して |x|≦M が成り立つことである．変数 x が無限小とは，任意の正の数 ε について |x|＜ε とできることである．

このような問題ではいかに「主語を補うか」ということがポイント．単に言葉の説明ではなく，用語の用法までを定義しなければならない．

結果

lim x = α を「無限小」という言葉を用いて定義せよ．

卒業生 N君の答

解答例

x-α が無限小．

無限小という言葉を使わなければ，「任意の正の数εについて|x-α|＜εとできる．」

結果

無限小と無限小の和が無限小であることを用いて，
lim(x+y) = lim x + lim y を示せ．

卒業生 N君の答

解答例

lim x = α，lim y = β とすると lim の定義から x-α が無限小， y-β が無限小．無限小と無限小の和が無限小であるから (x-α)+(y-β) も無限小． (x-α)+(y-β) = x+y-α-β = (x+y)-(α+β) が恒等式であることから， (x+y)-(α+β) も無限小再び lim の定義から lim (x+y)=α+βつまり lim(x+y)=lim x + lim y.

結果

数列 (1 + 1/n)^n の極限や， 2^(√3) の存在を保証する数列の定理はどのようなものか述べよ．

卒業生 N君の答

(1+1/n)^n の極限は e (自然対数)

この極限が自然対数の底 e であることは当然のことながら知識として持っていなければならない．しかしこの問題の意味は授業を受けていなければ，まったく不明だろう．

解答

定理：上に有界な単調増加数列は収束する．

数列 (1+1/n)^n は単調増加数列であり，上に有界な数列であることが示され，この定理によって極限値の存在がアプリオリに保証されるのである．そして存在が保証される極限値を使って定数 e が定義される．有理数の指数 2^(m/n) は n乗して 2^m になる正の実数ということで定義される．それを使って，数列 2^1, 2^1.7=2^(17/10), 2^1.73=2^(173/100), 2^1.732=2^(1732/1000) … を定義するとこの数列は単調増加で，つねに 2^2 より小さいので上に有界である．したがって，極限値が存在する．そして指数部分は √３に収束するから存在が保証されたこの数列の極限値を 2^(√3) と名づけるのである．