三角比とベクトルのつながりといえば,
余弦定理は「三平方の定理-2×内積」の形をしている,
などと思いだす方法を伝授することがある.>以前の記事「内積」
あるいは相関係数は cos の値のことだから,
相関係数=cos=内積÷大きさ
だよ.とかいろいろつなげて思い出す.自分は丸暗記できぬので,ほかのことから糸をたぐる.>以前の記事「相関係数=cosθ 」
そんなネタに,今までブログに書かなかったというか,書く機会がなかったけど,ふと思い出したのが,
「加法定理=内積」
2つの単位ベクトル\(\vec{x},\ \vec{y}\)を考える.
単位ベクトルは大きさ1のベクトルという意味だから,
\(|\vec{x}|=1,\ |\vec{y}|=1" alt="|\vec{x}|=1,\ |\vec{y}|=1\)である.
これらの横軸となす角がそれぞれ α,βだとすると,2つのベクトルのなす角は
\(\alpha-\beta\)であるから,内積の定義(大きさの積×コサイン)から
\(\vec{x}\cdot\vec{y}=|\vec{x}||\vec{y}|\cos(\alpha-\beta)\)
すなわち,
\(\vec{x}\cdot\vec{y}=1\times1\times\cos(\alpha-\beta)=\cos(\alpha-\beta)\)・・・(あ)
半径1 の円周上の,横軸とのなす角がθである点の座標は (cosθ, sinθ)であるから,
2つの単位ベクトル\(\vec{x},\ \vec{y}" alt="\vec{x},\ \vec{y}\)を成分表示すると,
\(\vec{x}=(\cos\alpha,\ \sin\alpha)\),\(\vec{y}=(\cos\beta,\ \sin\beta)" alt="\vec{y}=(\cos\beta,\ \sin\beta)\) である.
この成分で内積を計算すると,
\(\vec{x}\cdot\vec{y}=\cos\alpha\cos\beta+\sin\alpha\sin\beta\)
(あ)と合体させれば,
\(\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta\)
と三角関数の加法定理を得る.>くろべえ「加法定理」を含む記事
残りは
\(\sin(-\theta)=\sin\theta\)
\(\cos(-\theta)=\cos\theta\)
\(\sin(\frac{\pi}{2}-\theta)=\cos\theta\)
などを繰り返し使えば,全部導かれる.
数学はみんなつながってるw

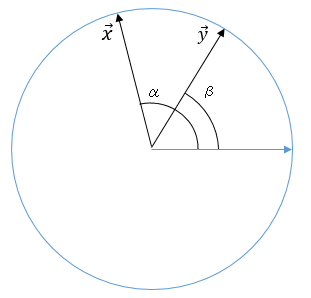
0 件のコメント:
コメントを投稿
スパム対策のため,コメントは,承認するまで表示されません。
「コメントの記入者:」は「匿名」ではなく,「名前/URL」を選んで,なにかニックネームを入れてください.URL は空欄で構いません.