教科書では
「x^2+2x+3=0 の解は，√(-2) が出てきて存在しないけど，云々」
という書き方をしている．
自分はもう少し突っ込んで，数学I の2次関数で習ったことから導入する．
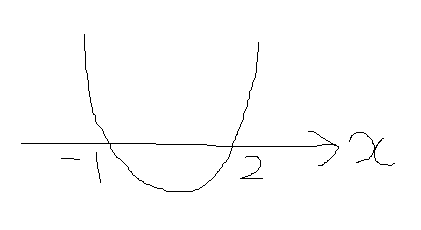
y=x^2-x-2 と x軸との交点の x 座標が 方程式 x^2-x-2=0 の解である．
でも，2次関数 y=x^2-2x+5 はx軸と出会わない．
このとき，√の中がマイナスになる．
だから，√の中がマイナスの数は，「数直線上にはない」
そして，教科書に戻る．教科書は，
「2乗して -1 になる新しい数を i とする」
と書いてあるけれど，自分はもう少し突っ込んで
「2乗して -1 になる数直線上にはない新しい数を i とする」
と付け加える．
あくまで，数直線上にないことを強調することを意識している．
「マイナス×マイナス だから，数直線の数の2乗はいつも0以上．2乗がマイナスになる i は数直線上にはない」
数直線上にないので1列に並べられず，大小もない．（正確には順序体ではない）
数直線上にはないけれど，平面上に表現できて，それが複素平面．
で，これをバリバリ使うのが物理や工学なわけだ．
電気や波動は複素数を使わねば面倒なことこの上ないし，量子論は本質的に複素数を使わねば表現できない．
このブログの複素数関係の記事＞Google検索
0 件のコメント:
コメントを投稿
スパム対策のため，コメントは，承認するまで表示されません。
「コメントの記入者:」は「匿名」ではなく，「名前/URL」を選んで，なにかニックネームを入れてください．URL は空欄で構いません．