8月に受けた試験の答えなど.
暗記問題,あるいは「公式暗記問題」ではあるが,理屈がわかればアタリマエのこと.物理というものはちょっとわかると全部アタリマエなのだ.
A-21 無変調時における送信電力(搬送波電力)が200〔W〕のDSB (A3E) 送信機が、特性インピーダンス50〔Ω〕の同軸ケーブルでアンテナに接続されている。この送信機の変調度を100〔%〕にしたとき、同軸ケーブルに加わる 電圧の最大値として、正しいものを下の番号から選べ。ただし、同軸ケーブルの両端は整合がとれているものとする。
1 105〔V〕
2 141〔V〕
3 200〔V〕
4 283〔V〕
5 400〔V〕
「A-13」と同じ,AM変調に関する計算問題.
えーっと,公式はあるだろうけど,そんなの覚えなくても,AM変調の意味からわかる.
搬送波電力200〔W〕を整合の取れたス50〔Ω〕の同軸ケーブルでアンテナに接続すれば,実効値電圧は,
$\sqrt{200\times50}=100$〔V〕
すると最大値電圧は
$100\sqrt{2}$〔V〕
これに100%の変調をかければ,さらに2倍の,
$200\sqrt{2}=200\times1.4142=282.84$〔V〕
答え:4
A-22 図に示すように、送信点B と受信点Cとの間の距離が600〔km〕で、電離層のF層1回反射伝搬において、最高使用可能周波数(MUF) が20〔MHz〕であるとき、臨界周波数$f_c$〔MHz〕の値として、正しいものを下の番号から選べ。ただし、F層の反射点Aの高さは400〔km〕とする。また、MUF を$f_m$〔MHz〕とし、θ を電離層への入射角及び反射角とすれば、$f_m$は、次式で与えられるものとする。
$f_m = f_c \sec\theta$
1 18〔MHz〕
2 16〔MHz〕
3 14〔MHz〕
4 12〔MHz〕
5 10〔MHz〕
「正割の法則」とよばれる公式がついている.
反射点Aの真下までの水平距離は 600÷2=300〔km〕からABの長さはピタゴラスの定理で,$\sqrt{300^2+400^2}=500$〔km〕から,
$20=f_c\sec\theta = f_c \frac{500}{400}$
$f_c=20\times\frac{4}{5}=16$〔MHz〕
答え:2
「正割sec」 とは余弦cos の逆数.高校の教科書から「正割」が消えた現在,いまだにその名の法則名が使われているのか・・・
これを高校の教科書で載せるなら(ありえないけど),
$f_c = f_m \cos\theta$
などとして,「余弦の法則」とでもするん?
というより,「法則」と名づけるほどのものなのかねぇ.ただの三角比(数I)だろうに.
A-23 次の記述は、超短波(VHF) 帯電波伝搬における山岳回折波について述べたものである。 内に入れるべき字句の正しい組合せを下の番号から選べ。
(1) 電波の伝搬路上に山岳があるとき、山岳の尾根の厚みが波長に比べて A 、かつ、完全導体と見なせるような場合には、山岳回折波の電界強度は、山岳がないとした場合の球面大地回折波より著しく B なることがある。
(2) 山岳回折波に生ずるフェージングの強さは、伝搬路上に山岳がない場合の通常のフェージングよりも C 。
A B C
1 厚く 強く 弱い
2 厚く 弱く 強い
3 厚く 弱く 弱い
4 薄く 弱く 強い
5 薄く 強く 弱い
答え:5
物理(波の回折)を知っていれば,薄いほうが回折しやすいし,球面回折より強くなるのは常識.
しかし試験当日は「100%の自信」はなかった.
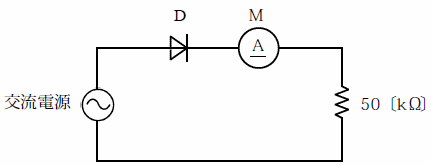
A-24 図に示す単相半波整流回路において、交流電源電圧の波形が正弦波でその実効値が100〔V〕のとき、負荷抵抗50〔k Ω〕に 流れる電流を平均値指示形の電流計M で測定した。このときのMの指示値として、最も近いものを下の番号から選べ。ただし、M の内部抵抗及びダイオードDの順方向抵抗の値は零であり、Dの逆 方向抵抗の値は無限大とする。
1 0.5〔mA〕
2 0.9〔mA〕
3 1.5〔mA〕
4 1.8〔mA〕
5 2.0〔mA〕
半波整流なので,実効値電圧は単純に半分の100〔V〕となり,実効値電流もオームの法則で,50÷50000=0.001=1〔mA〕
これを平均値指示形の電流計で測る.
実効値1〔mA〕のとき,最大値は√2〔mA〕そのとき平均値は√2×2÷π=0.900316316〔mA〕.
答え:2
平均値指示形とは「ふつうの」電流計のこと.直流なら,実効値=平均値だけれど,交流は,最大値=実効値×√2=平均値×π÷2になるから換算が必要.
その理屈,最大値と実効値と平均値の関係は,三角関数の積分で説明がつく.
基本は面積(積分)÷幅=高さの平均ということ.
交流電圧をsinとすると最大値は 1
このとき
$\int_0^\pi \sin x\,dx=2$
である.つまりsinの上半分
 の幅π,高さ1,面積2 だから,これを平らに均すと平均は面積を幅で割って,2÷π.
の幅π,高さ1,面積2 だから,これを平らに均すと平均は面積を幅で割って,2÷π.この最大値1〔V〕の交流電圧(sin)を負荷は1〔Ω〕にかければ1〔A〕の交流電流(sin)が流れ,その交流電力は
電力=電圧×電流 より 交流の電力=sin×sin
$\int_0^\pi\sin^2 x\,dx=\frac{\pi}{2}$
より電力曲線 sin^2
 の平均は (π/2)÷π=1/2〔W〕
の平均は (π/2)÷π=1/2〔W〕実効値は「直流電力と同じ」ということ.
したがって,最大値電圧1〔V〕,最大値電流1〔A〕の交流の平均電力が 1/2〔W〕と同じ直流になるには,今,負荷が1〔Ω〕だから電圧も電流も同じ数値になり,直流電圧1/√2〔V〕,直流電流1/√2〔A〕となる.
つまり,
交流の最大値×(1/√2)=実効値(直流と同じ)
なのである.よって,
最大値=実効値×√2
ここで,
平均値=最大値×2÷π
だったから,
平均値=(実効値×√2)×2÷π=1〔mA〕×√2×2÷π=0.900316316
こういう理屈を知っていれば,公式の暗記は不要だが,まぁ,普通は最後の式を「公式」として暗記して試験を受けるわけだ.
A-25 次の記述は、スーパヘテロダイン方式スペクトルアナライザについて述べたものである。このうち誤っているものを下の番号から選べ。
1 分解能帯域幅を変えて測定することができる。
2 入力信号の周波数成分ごとの振幅を観測できる。
3 表示器の横軸は振幅を、また、縦軸は周波数を表す。
4 オシロスコープと比べて感度が高いので、より弱いレベルの信号の測定ができる。
答え:3
これは,理屈ではなくスペクトルアナライザの暗記問題.
スペクトルというのは,虹の色みたいなものだから,光をプリズムで分解したら,横方向に広げて観測すものだ.と思えれば,3が誤りであることがわかる.
でももし,「3」の通りなら,表示部が縦長になって,見づらいだろうなぁ.
>つづく
無線工学 A-1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 B-1 2 3 4 5
法規 A-1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 B-1 2 3 4 5


![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/02df043e.e9642a47.0402c1c1.56cd9be5/?me_id=1213310&item_id=19343773&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F3102%2F9784501333102_1_3.jpg%3F_ex%3D128x128&s=128x128&t=picttext)









































